文章目录
头指针:
1)头指针是指链表中 ,指向第一个结点的指针(可以是头结点也可以是首元节点,看实现方式)
2)头指针是必须存在的,链表为空也存在(head=null)
头结点(虚拟头结点/哨兵节点/哑节点)
1)数据域可以不存信息,也可以存储长度等附加信息
2)头结点不是必须的,一般设置头结点是为了简化编程处理统一逻辑,有头结点的情况,头指针指向头结点(head.next==dummyHead)
首元节点
链表中存储实际数据的第一个元素
三者关系图

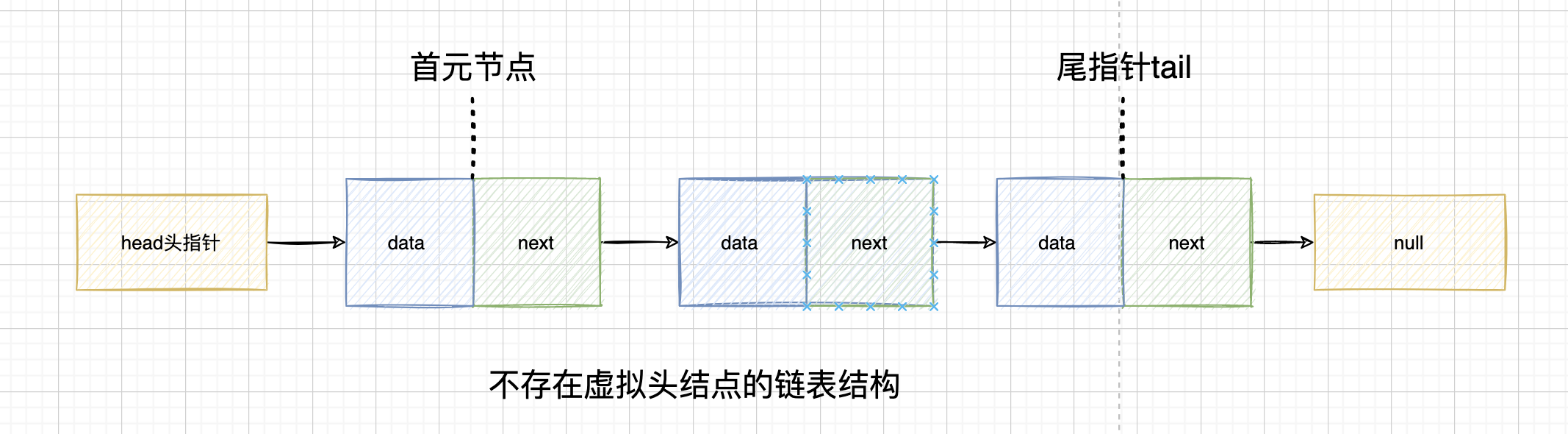
判断链表为空
带头结点的单链表的判空:head.next == null;
不带头结点的单链表的判空:head == null;
一、遍历
//head 如果链表为空,那就是null public void traverse() { Node p = head; //不能p.next!=null 很可能p本身就null,而且重点要遍历到最后一个元素 while (p != null) { System.out.print(p.data + "->"); p = p.next; } System.out.println(); } 二、查找
public Node find(int value) { Node p = head; //不能p.next!=null 很可能p本身就null,而且重点要遍历到最后一个元素 while (p != null) { if (p.data == value) { return p; } p = p.next; } return null; } 三、插入
1、链表头部插入
需要注意的是:
-
头部插入 遍历的时候 与输入顺序相反 最后一个插入的最先遍历
-
头插法不需要判断链表是否为空,链表为空,也是满足下面的代码的
public void insertAtHead(int value) { Node newNode = new Node(value); if (head != null) { newNode.next = head; } head = newNode; } 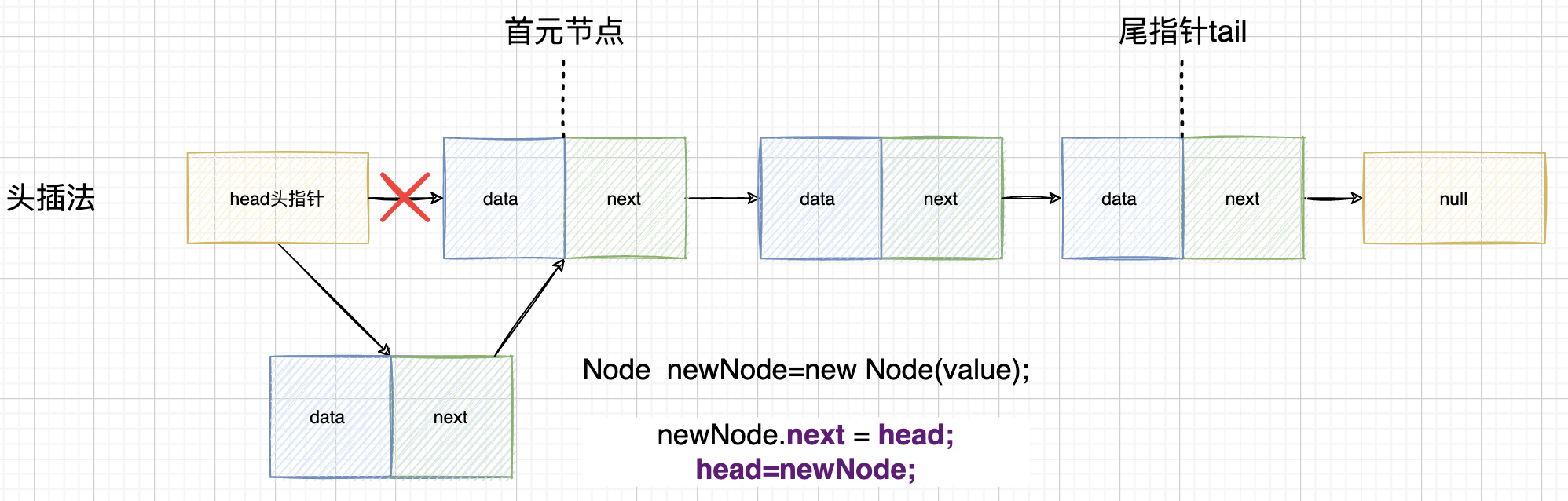
2、链表尾部插入
我们可以发现插入操作是O(N) 每次都要遍历到最后,所以可以进行下面的优化–添加tail尾节点
//(data,next) //head->1 ->2->3->null //head->null public void insertAtTail(int value) { Node newNode = new Node(value); //特殊处理链表为空的情况 if (head == null) { head = newNode; } else { Node p = head; //这里不能改成p!=null,因为改成这个的话,直接遍历到最后一个节点,但是并没有前后连接起来:用next while (p.next != null) { p = p.next; } p.next = newNode; } } 1)优化1:添加tail尾节点
这里我们添加尾结点优化每次需要遍历
但是我们发现这里还有个问题就是每次需要特殊处理链表为空的情况,其实我们可以使用上面的虚拟头结点来进行优化
public Node head; public Node tail; //添加尾结点优化每次需要遍历 //尾插法优化1:添加尾节点 //head->1 ->2->3->null //head->null public void insertTailPlus1(int value) { Node newNode = new Node(value); //特殊处理链表为空的情况 if (head == null) { head = newNode; tail = head; } else { tail.next = newNode; tail = newNode; } } 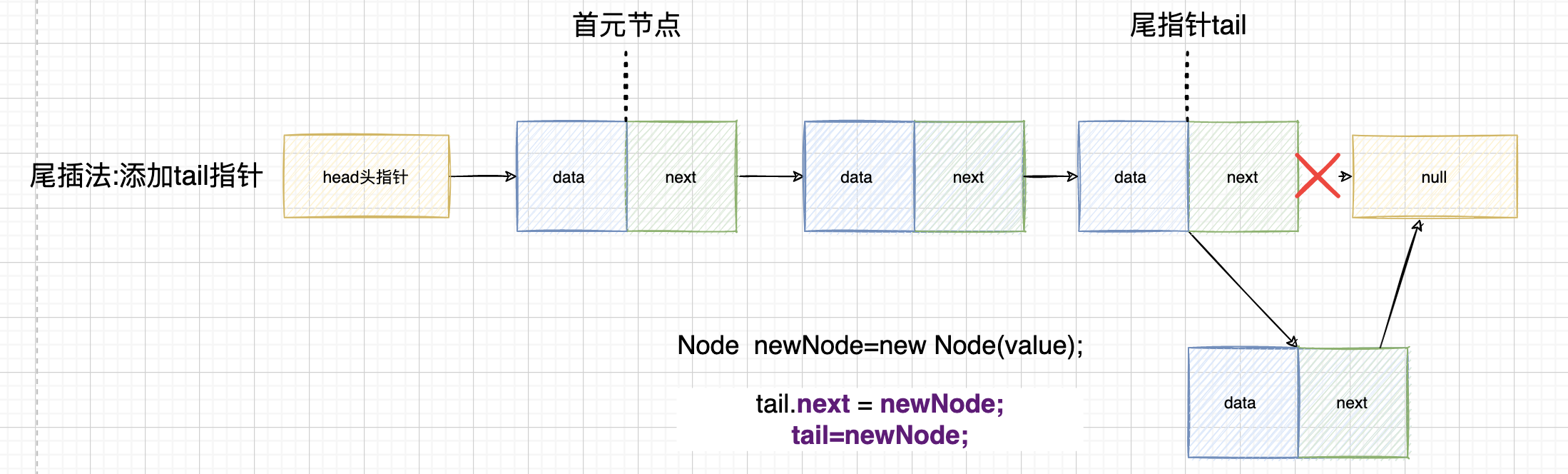
2)优化2:添加虚拟头结点
这里我们添加虚拟头结点进行优化
public Node newHead = new Node(); //添加虚拟头结点 public Node newTail = newHead; //相当于newTail一直往后塞数据,但是虚拟头结点还是不变的 //尾插法优化2:添加虚拟头结点 //head->1 ->2->3->null //head->null public void insertTailPlus2(int value) { Node newNode = new Node(value); newTail.next = newNode; newTail = newNode; //由于遍历的时候使用head,将newHead.next也就是第一个实际的元素指向head,其实只要赋值一次即可 //如果不用head头指针遍历,用newHead进行遍历,不需要添加这个 //head = newHead.next; } 图解可参考上面,只是不需要考虑head==null的情况
3、给点节点后插入
//指定节点后面插入 //head->1 ->2->3->null //head->null public void insertAfterThisNode(Node p, int value) { Node newNode = new Node(value); //指定节点是空直接不用处理 if (p == null) { return; } newNode.next = p.next; p.next = newNode; } 四、删除
1、删除指定节点后面的节点
//删除指点节点的下一个节点 //head->1 ->2->3->null //head->null public void deleteNextNode(Node p) { //如果是最后一个节点或者节点不存在就不需要处理 if (p == null || p.next == null) { return; } p.next = p.next.next; } 2、删除指定节点
我们知道删除指定节点的时候需要知道前驱节点,所以最主要是在遍历的过程中时刻保存待删除节点的前驱节点
这个逻辑稍微复杂点,思路如下:
1)定义一个变量prev时刻保存待删除节点的前驱节点
2)遍历链表,当找到待删除节点的时候跳出循环,没有的话就用prev时刻保存前驱节点
3)判断是否找到了最后还没找到待删除节点 比如Node node=new Node(99999999);不存在,直接返回
4)这时候要进行判断prev的情况
- 前驱节点为空,说明删除的是头结点,则head=head.next即可
- 前驱节点不为空,说明是正常删除,直接prev.next=prev.next.next
//删除指定节点 //head->1 ->2->3->null //head->null public Node deleteThisNode(Node thisNode) { if (head == null || thisNode == null) { return null; } Node p = head; Node prev = null; //这里有可能要删除的就是最后一个节点 这时候 p.next!=null已经不满足条件会跳出,所以要用p!=null判断 while (p != null) { if (p == thisNode) { break; } //保存每次向后移 之前的前驱节点 prev = p; p = p.next; } //找到了最后还没 比如Node node=new Node(99999999);不存在 if (p == null) { return null; } //说明删除的是头结点,第一次进入while就break了,头结点没有前驱节点,所以直接将头结点向后移一位即可 if (prev == null) { head = head.next; } else { //删除非头结点 prev.next = prev.next.next; } return head; } 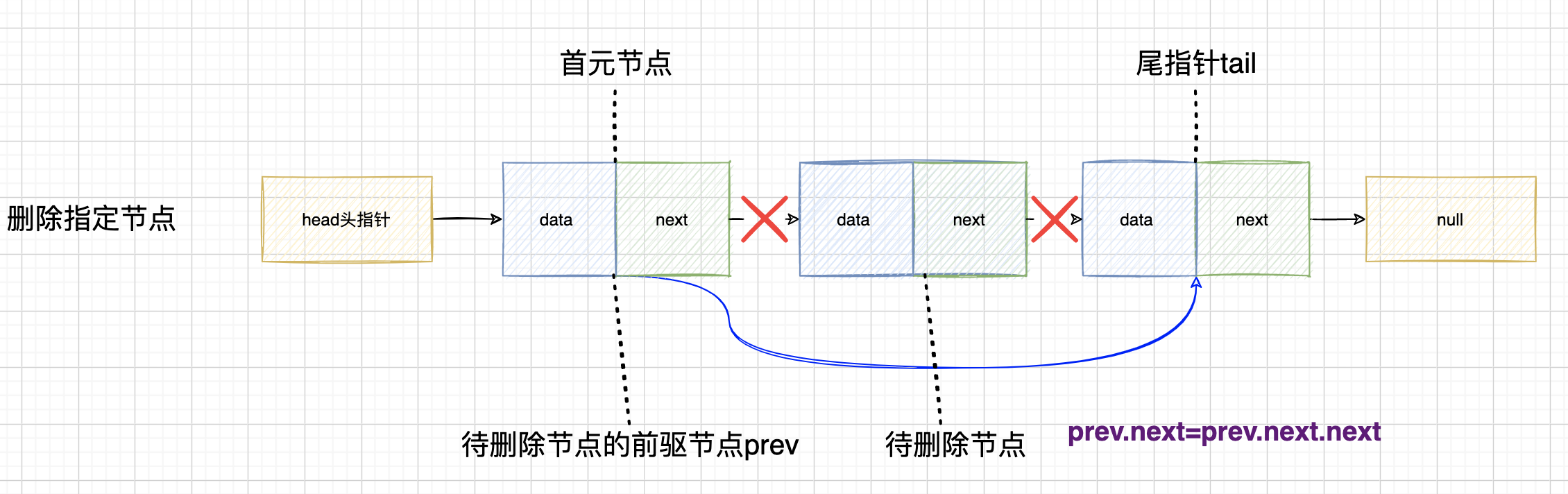
虚拟头结点优化
前面逻辑有个修改就是前驱节点从虚拟头结点开始而不是null,所以在最后面不需要对prev进行判空了,因为链表为空,有了虚拟头节点prev.next = prev.next.next;也是符合的
public Node deleteThisNodePlus(Node thisNode) { if (head == null || thisNode == null) { return null; } newHead.next = head; Node prev = newHead; //前驱节点从虚拟头结点开始而不是null Node p = head; while (p != null) { if (p == thisNode) { break; } prev = p; p = p.next; } if (p == null) { return null; } prev.next = prev.next.next; return newHead.next; } 五、根据索引下标插入删除
这部分代码就不在做过多的解释,如果上面理解了,下面这个也能很好的理解,直接贴代码
//根据索引下标插入值 //head->1 ->2->3->null //head->null public void insertAtIndex(int index, int value) { if (index < 0 || index > count) { return; } Node newNode = new Node(value); Node p = head; if (head == null) { head = newNode; count++; } else { int k = 0; while (p != null) { if (k == index) { newNode.next = p.next; p.next = newNode; count++; return; } k++; p = p.next; } } } //删除指定下标 //head->1 ->2->3->null //head->null public void deleteAtIndex(int index) { if (index < 0 || index > count || head == null) { return; } Node p = head; int k = 0; Node prev = null; while (p != null) { if (k == index) { count--; break; } k++; prev = p; p = p.next; } //没找到 if (p == null) { return; } if (prev == null) { head = head.next; } else { prev.next = prev.next.next; } } 六、时间复杂度分析
我们经常听到说数组查询快、插入删除慢;链表插入删除快、查询慢;
其实这都是不完整的,我们说数组查询快,说的是根据下标随机访问时间复杂度是O(1),而如果具体我们要找某个值,还是要遍历整个数组
链表插入删除快,也是有前提的,要在知道前驱节点的情况,插入删除才是O(1);如果不知道的话,还是要遍历链表找到待删除节点的前驱节点
这里贴上完整的代码和对应每个方法的测试如下,可以直接运行
package com.apple; import org.junit.Test; /** * @author Apple * @date 2021-12-10 22:07 **/ public class MyLinkedList { public Node head; public Node tail; public int count; public Node newHead = new Node(); public Node newTail = newHead; //相当于newTail一直往后塞数据,但是虚拟头结点还是不变的 //head 如果链表为空,那就是null public void traverse() { Node p = head; //不能p.next!=null 很可能p本身就null,而且重点要遍历到最后一个元素 while (p != null) { System.out.print(p.data + "->"); p = p.next; } System.out.println(); } public void insertAtHead(int value) { Node newNode = new Node(value); if (head != null) { newNode.next = head; } head = newNode; /* if (head == null) { head = newNode; } else { newNode.next = head; head = newNode; }*/ } //(data,next) //head->1 ->2->3->null //head->null public void insertAtTail(int value) { Node newNode = new Node(value); if (head == null) { head = newNode; } else { Node p = head; //这里不能改成p!=null,因为改成这个的话,直接遍历到最后一个节点,但是并没有前后连接起来:用next while (p.next != null) { p = p.next; } p.next = newNode; } count++; } //尾插法优化1:添加尾节点 //head->1 ->2->3->null //head->null public void insertTailPlus1(int value) { Node newNode = new Node(value); if (head == null) { head = newNode; tail = head; } else { tail.next = newNode; tail = newNode; } count++; } //尾插法优化2:添加虚拟头结点 //head->1 ->2->3->null //head->null public void insertTailPlus2(int value) { Node newNode = new Node(value); newTail.next = newNode; newTail = newNode; //由于遍历的时候使用head,将newHead.next也就是第一个实际的元素指向head,其实只要赋值一次即可 head = newHead.next; count++; } //指定节点后面插入 //head->1 ->2->3->null //head->null public void insertAfterThisNode(Node p, int value) { Node newNode = new Node(value); if (p == null) { return; } newNode.next = p.next; p.next = newNode; count++; } //删除指点节点的下一个节点 //head->1 ->2->3->null //head->null public void deleteNextNode(Node p) { if (p == null || p.next == null) { return; } p.next = p.next.next; count--; } //删除指定节点 //head->1 ->2->3->null //head->null public Node deleteThisNode(Node thisNode) { if (head == null || thisNode == null) { return null; } Node p = head; Node prev = null; //这里有可能要删除的就是最后一个节点 这时候 p.next!=null已经不满足条件会跳出,所以要用p!=null判断 while (p != null) { if (p == thisNode) { break; } //保存每次向后移 之前的前驱节点 prev = p; p = p.next; } //找到了最后还没 比如Node node=new Node(123);不存在而不是null if (p == null) { return null; } //说明删除的是头结点,第一次进入while就break了 头结点没有前驱节点 if (prev == null) { head = head.next; } else { //删除非头结点 prev.next = prev.next.next; } count--; return head; } public Node deleteThisNodePlus(Node thisNode) { if (head == null || thisNode == null) { return null; } newHead.next = head; Node prev = newHead; //前驱节点从虚拟头结点开始而不是null Node p = head; while (p != null) { if (p == thisNode) { break; } prev = p; p = p.next; } if (p == null) { return null; } prev.next = prev.next.next; count--; head=newHead.next; return head; } //根据索引下标插入值 //head->1 ->2->3->null //head->null public void insertAtIndex(int index, int value) { if (index < 0 || index > count) { return; } Node newNode = new Node(value); Node p = head; if (head == null) { head = newNode; count++; } else { int k = 0; while (p != null) { if (k == index) { newNode.next = p.next; p.next = newNode; count++; return; } k++; p = p.next; } } } //删除指定下标 //head->1 ->2->3->null //head->null public void deleteAtIndex(int index) { if (index < 0 || index > count || head == null) { return; } Node p = head; int k = 0; Node prev = null; while (p != null) { if (k == index) { count--; break; } k++; prev = p; p = p.next; } //没找到 if (p == null) { return; } if (prev == null) { head = head.next; } else { prev.next = prev.next.next; } } public Node find(int value) { Node p = head; //不能p.next!=null 很可能p本身就null,而且重点要遍历到最后一个元素 while (p != null) { if (p.data == value) { return p; } p = p.next; } return null; } class Node { public int data; public Node next; public Node(int data, Node next) { this.data = data; this.next = next; } public Node(int data) { this.data = data; } public Node() { } } //头插法:初始化插入链表 @Test public void testInsertAtHead() { //头插法:初始化插入链表 insertAtHead(1); insertAtHead(2); insertAtHead(3); //遍历链表 traverse(); Node findNode = find(3); System.out.println(findNode.data); } //尾插法:初始化 @Test public void testInsertAtTail() { insertAtTail(1); insertAtTail(2); insertAtTail(3); //遍历链表 traverse(); Node findNode = find(3); System.out.println(findNode.data); } //尾插法优化1:添加尾节点 @Test public void testInsertTailPlus1() { insertTailPlus1(1); insertTailPlus1(2); insertTailPlus1(3); //遍历链表 traverse(); Node findNode = find(3); System.out.println(findNode.data); } //尾插法优化2:添加虚拟头节点 @Test public void testInsertTailPlus2() { insertTailPlus2(1); insertTailPlus2(2); insertTailPlus2(3); //遍历链表 traverse(); Node findNode = find(3); //System.out.println(findNode.data); } //指定节点后面插入 @Test public void testInsertThisNode() { insertTailPlus2(1); insertTailPlus2(2); insertTailPlus2(3); Node findNode = find(2); insertAfterThisNode(findNode, 999); //找一个不存在的值插入 Node findNullNode = find(222); insertAfterThisNode(findNullNode, 111); traverse(); } //删除指定节点之后的节点 @Test public void testDeleteNextNode() { insertTailPlus2(1); insertTailPlus2(2); insertTailPlus2(3); Node findNode = find(2); deleteNextNode(null); deleteNextNode(findNode); //找一个不存在的值插入 traverse(); } //删除指定节点 //1->2->3 :删除4 删除1 2 3 //1、比如删除的刚好就是最后一个3 带进去看看符不符合 删除1就是删除头结点 //链表只有一个元素 1 删除1 就是删除头结点:prev=null @Test public void testDeleteThisNode() { insertTailPlus2(1); //insertTailPlus2(2); //insertTailPlus2(3); Node findNode = find(1); Node findNode2 = new Node(3); deleteThisNode(findNode); //deleteThisNode(findNode2); //找一个不存在的值插入 traverse(); } //删除指定节点 //1->2->3 :删除4 删除1 2 3 //1、比如删除的刚好就是最后一个3 带进去看看符不符合 删除1就是删除头结点 //链表只有一个元素 1 删除1 就是删除头结点:prev=null @Test public void testDeleteThisNodePlus() { insertTailPlus2(1); insertTailPlus2(2); insertTailPlus2(3); Node findNode = find(2); Node findNode2 = new Node(3); deleteThisNodePlus(findNode); //deleteThisNode(findNode2); //找一个不存在的值插入 traverse(); } @Test public void testInsertAtIndex() { insertAtIndex(0, 6); insertAtIndex(0, 7); insertAtIndex(0, 20); insertAtIndex(5, 11); //insertAtIndex(0,6); //insertTailPlus2(2); //insertTailPlus2(3); //Node findNode = find(1); //deleteThisNode(findNode2); //找一个不存在的值插入 traverse(); } @Test public void testDeleteAtIndex() { insertTailPlus1(1); insertTailPlus1(2); insertTailPlus1(3); deleteAtIndex(5); //不存在的 deleteAtIndex(1); //Node findNode = find(1); //找一个不存在的值插入 traverse(); System.out.println(count); } } 下一个:Lambda8 表达式
热门文章
- 宠物店最怕什么投诉才会退款 宠物买卖纠纷找哪个部门协调
- 1月4日20.4M/S|SSR/Clash/Shadowrocket/V2ray免费节点每天更新链接地址,便宜机场推荐
- 1月5日18.1M/S|SSR/V2ray/Shadowrocket/Clash免费节点每天更新链接地址,便宜机场推荐
- 2月24日18.8M/S|Clash/SSR/V2ray/Shadowrocket免费节点每天更新链接地址,便宜机场推荐
- 宠物医院加盟好还是自己开好(宠物医院加盟好还是自己开好一点)
- 饲料厂饲料机设备多少钱一套(饲料机器多少钱一台)
- 1月12日20.6M/S|Clash/V2ray/SSR/Shadowrocket免费节点每天更新链接地址,便宜机场推荐
- 湖北领养狗狗多少钱(湖北襄阳免费领养狗)
- 2月20日20.8M/S|SSR/Shadowrocket/V2ray/Clash免费节点每天更新链接地址,便宜机场推荐
- 慢SQL,压垮团队的最后一根稻草